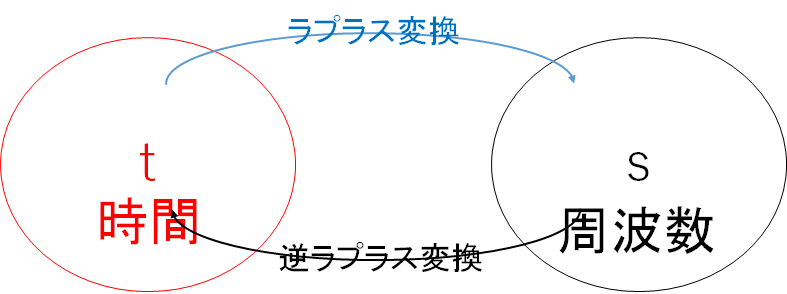
この章の最初に、ラプラス変換を使うと微分方程式を四則演算で解ける、といいました。ラプラス変換を使って微分方程式解くときの基本的な流れは以下の図の通りです。 与えられた $y(t)$ の微分方程式をラプラス変換することにより、$Y(s)$ の代数方程式に持ち込んでそれを解き、その後整理された $Y(s)$ をラプラス逆変換して解となる $y(t)$ を求めることになります。 では、次の一階線形微分方程式をラプラス変換を使って解いてみます。 $ y'(t) - 2y(t) = e^{t} 　　(y(0)= 1)$ まずは両辺をラプラス変換します。 $L[y'(t) - 2y(t)] = L[e^t] $ $sY(s) - y(0) - 2Y(s) = \dfrac{1}{s-1}$ $sY(s) - 1 - 2Y(s) = \dfrac{1}{s-1}　　※y(0)= 1$ $(s-2)Y(s) = \dfrac{1}{s-1} + 1 $ $Y(s) = \dfrac{1}{(s-1)(s-2)} + \dfrac{1}{s-2} $ これから $Y(s)$ を整理します。まずは $ \dfrac{1}{(s-1)(s-2)} $ の部分分数展開について説明しましょう。 部分分数展開するには、$ \dfrac{1}{(s-1)(s-2)} = \dfrac{A}{s-1} + \dfrac{B}{s-2}$ とおきます。 $\dfrac{A}{s-1} + \dfrac{B}{s-2}$ $ = \dfrac{(s-2)A + (s-1)B}{(s-1)(s-2)} $ $ = \dfrac{(A + B)s -2A -B}{(s-1)(s-2)} $ この式が、$ \dfrac{1}{(s-1)(s-2)} $と同じになるので、 $ \begin{eqnarray} \left\{ \begin{array}{l} A + B = 0 \\ -2A - B = 1 \end{array} \right. \end{eqnarray} $ となり、この連立方程式を解くと、$ A = -1,　B = 1$ となります。よって、 $ \dfrac{1}{(s-1)(s-2)} = \dfrac{-1}{s-1} + \dfrac{1}{s-2}$ となることが分かりました。なので、 $Y(s)$ は以下のように展開できますね。 $Y(s) = \dfrac{-1}{s-1} + \dfrac{1}{s-2} + \dfrac{1}{s-2} $ $　　= \dfrac{2}{s-2} - \dfrac{1}{s-1} $ $Y(s)$ が整理できたので、これをラプラス逆変換して $y(t)$ を求めます。 $ y(t) = L^{-1}[Y(s)] = 2 L^{-1}[\dfrac{1}{s-2}] - L^{-1}[\dfrac{1}{s-1}] $ 　　$= 2e^{2t} -e^t $ これで $y(t)$ が求まりました。 微分方程式とラプラス変換について、さらに詳しく学びたい方には、以下の本がおすすめです（楽天のサイトにとびます）。

　ラプラス変換はデルタ関数やステップ関数についても応用することができます。デルタ関数やステップ関数の基本について学びたい方は、以下の動画をどうぞ。 デルタ関数とステップ関数のラプラス変換は以下のように表されます。 上記のラプラス変換が成り立つことを確認してみましょう。 まずはデルタ関数のラプラス変換です。 $L[\delta (t-a)]　(a ≧ 0) $ について考えてみましょう　($L[\delta (t)] = 1 $ は $L[\delta (t-a)]　(a ≧ 0)$ の $a$ に $0$ を代入したものです)。 ラプラス変換の定義式は $F(s) = \displaystyle \int_0^\infty e^{-st} f(t) dt$ なので、デルタ関数 $\delta (t-a)$ のラプラス変換は以下のようになりますね。 $L[\delta (t-a)] = \displaystyle \int_0^\infty e^{-st} \delta (t-a) dt $ ここで、この式にある公式を当てはめたいと思います。 公式１　　$ \displaystyle \int_{-\infty}^{ \infty } f(t) \delta (t-a) dt = f(a) $ この公式は積分区間が $ -\infty $ から $ \infty $ までなので、先ほどのデルタ関数のラプラス変換とは積分区間が異なります。ですが、デルタ関数は以下の図のように、$ t \lt 0 $ のとき $ \delta (t-a) = 0 $ なので、tの積分区間を $ -\infty $ から $ \infty $ にしても結果は変わりません。 よって、 これで、上の公式１が適用できます。$f(t) = e^{-as} $ と考えると $\displaystyle \int_{-\infty}^{\infty} e^{-st} \delta (t-a) dt = e^{-as} $ となります。これまでは $L[\delta (t-a)] $ を考えてきましたが、$L[\delta (t)] $　はこの結果に $ a = 0 $ を代入して $ e^0 = 1 $。これで $L[\delta (t)] = 1 $ であることが確認できました。

　ブロムウィッチ積分を使うことで逆ラプラス変換の公式を求めることができます。 ラプラス逆変換の公式は以下のようになります。そして、これこそが、ブロムウィッチ積分の正体なのです。 おさらいとして、フーリエの積分定理についても簡単に書いておきます。詳しく学びたい方はフーリエの積分定理の章を確認ください。 $g(t)$ が $-∞$ から $∞$ で区分的に滑らかで、かつ絶対可積分であるとき、 \[g(t) = \frac{1}{2 \pi} \displaystyle \int_{-\infty}^{\infty} e^{i\alpha t} \{\displaystyle \int_{-\infty}^{\infty} g(t) e^{-i\alpha t} dt \} d\alpha \] が成り立ちます。これがフーリエの積分定理でした。 これから、ブロムウィッチ積分が成り立つことを確認していきます。まず、定積分 $ \displaystyle \int_{p-i\omega}^{p+i\omega} F(s) e^{st} ds$ を考えます。 $s = p+ i\alpha$ のとき、$s→\alpha$ で、$s$ が $p-i\omega$ から $p+i\omega$ のとき、$\alpha$ は $-\omega　→　\omega$ となります。そして、$ds = id\alpha$ です。また、ラプラス変換の定義は $ F(s) = \displaystyle \int_{0}^{\infty} f(t) e^{-st} dt$ なので、 $ \displaystyle \int_{p-i\omega}^{p+i\omega} F(s) e^{st} ds = \displaystyle \int_{-\omega}^{\omega} \{\displaystyle \int_{0}^{\infty} f(t) e^{-st} dt \} e^{(p+i\alpha)t} id\alpha $ $e^{(p+i\alpha)t}$ は $e^{pt} \cdot e^{i\alpha t}$ なので $ = ie^{pt} \displaystyle \int_{-\omega}^{\omega} e^{i\alpha t} \{\displaystyle \int_{0}^{\infty} f(t) e^{-(p+i\alpha)t} dt \} d\alpha $ $e^{-(p+i\alpha)t} $ は $e^{-pt} \cdot e^{i\alpha t}$ なので ここで、$ \omega → \infty $ の極限を取って、 $ \displaystyle \lim_{ \omega \to \infty } \displaystyle \int_{p-i\omega}^{p+i\omega} F(s) e^{st} ds $ $ \displaystyle \int_{p-i\infty}^{p+i\infty} F(s) e^{st} ds $ $ = ie^{pt} \displaystyle \int_{-\infty}^{\infty} e^{i\alpha t} \{\displaystyle \int_{-\infty}^{\infty} e^{-i\alpha t} (e^{-pt} f(t)) dt \} d\alpha $ $ e^{-pt} f(t) $を　$ g(t) $ とおき、さらにフーリエの積分定理の形に近づけて、 $ = 2\pi ie^{pt} \frac{1}{2\pi} \displaystyle \int_{-\infty}^{\infty} e^{i\alpha t} \{\displaystyle \int_{-\infty}^{\infty} g(t) e^{-i\alpha t} ) dt \} d\alpha $ 式の中に、フーリエの積分定理( $ g(t) = e^{-pt} f(t) $ )が現れたので、 $ 2\pi ie^{pt} e^{-pt} f(t) = 2\pi i f(t) $ よって、 $ 2\pi i f(t) = \displaystyle \int_{p-i\infty}^{p+i\infty} F(s) e^{st} ds $ $ f(t) = \dfrac{1}{2\pi i} \displaystyle \int_{p-i\infty}^{p+i\infty} F(s) e^{st} ds $ これで、ブロムウィッチ積分が成り立つことが分かりました。